首先说明一下这一系列的文章内容
我是从 Deep Learning（花书）入门深度学习的，在书中讲述了很多数学的原理和深度学习网络的工作原理，里面的推导内容有些难懂，对于线性代数半吊子我来说有些不能理解，需要通过实践才能才能有更透彻的推导和理解
而且在网上找了很多关于深度学习的东西，适合入门理解和学习的东西并不多，我希望我的这一些小记录能帮到想要了解深度学习的朋友

一维线性回归

入门机器学习最基础的东西既是线性回归，即有如下形式的方程：

$\vec y = W\vec x+b$

其中 $\vec y$ 是输出， $\vec x$ 是输入， $W$ 是系数矩阵(weights)， $b$ 是置偏(bias)

这是多维的线性方程，我们接下来要研究的是以上公式的简化版本：

$y=wx$

上面的 $y,w,x$ 都是一维的标量

我们要学习就是我们平时看到的一次函数。
我们要实现的是我们给计算机一系列的 $x,y$ 的值，让计算机自己找到(学习)这个 $w$ 的值。

基本的算法

代码流程

这里我利用numpy来处理数值问题，利用matplotlib来简单展示数据

1 2	import numpy as np import matplotlib.pyplot as plt

生成训练数据，标准的 $w'=1$

W_ = 1.0
data_size = 20
X = np.linspace(0, 10, data_size+1)
Y = W_*X
plt.scatter(X, Y)
plt.show()

初始化待训练的数据

1	w = 0 #待训练的参数w

训练代码：

step_num = 301		#训练用的步数
learning_rate = 0.001	#之后进行介绍
loss_per_step = []
total_loss = 0
for i in range(step_num):
    x, y_ =  X[i%data_size], Y[i%data_size]
    y = w * x
    loss = math.sqrt((y-y_)**2)
    loss_per_step.append(loss)
    if y-y_ >0:
        w = w - x * learning_rate
    elif y-y_<0:
        w = w + x * learning_rate
print (w)

代码解释

我们训练训练300次，每次训练按照之前给的流程图的步骤走

获取一对数据 $x,y'$
根据我们的模型计算拟合出来的 $y$ 值

之后计算拟合出来的 $y$ 和 $y'$ 之间的距离:

$loss=\sqrt{(y-y')^2}$

这是我们评估模型准确度的标准，我们一般把这种函数称为损失函数(loss)

我们模型跟数据情况符合的越好，我们的loss值应该就越低。

接下来就我们的目标就是调整我们的参数 $w$ ，让 $loss$ 尽量的小，那么我们就得研究当 $w$ 变化时 $loss$ 是如何变化的( $x,y$ 都不是我们的研究对象，可看做定值)。
由上面的公式有如下关系：

$\begin{aligned} loss=\sqrt{(wx-y')^2} \\ \quad\ =|(wx-y')^2| \end{aligned}$

我们让 $loss$ 对 $w$ 求导:

$\frac{\mathrm{d}}{\mathrm{d}w}loss=\left\{ \begin{aligned} x, wx-y'>0 \\ -x, wx-y'<0 \end{aligned} \right.$

导数的方向是 $loss$ 增大的方向，所以我们是每一步调整 $w$ 使的 $loss$ 变小，我们用以下的式子来更新 $w$ :

$w_{updated} = w_{old} - \epsilon \frac{\mathrm{d}}{\mathrm{d}w}loss$

即向 $loss$ 导数的负方向移动一小步， $\epsilon$ 就是上面代码中的学习率(leaning rate)

我们在代码中用loss_per_step记录了每一步的 $loss$ 变化，用以下代码展示出来：

1
2
3

steps = np.linspace(0, step_num, len(loss_per_step))
plt.plot(steps, loss_per_step)
plt.show()

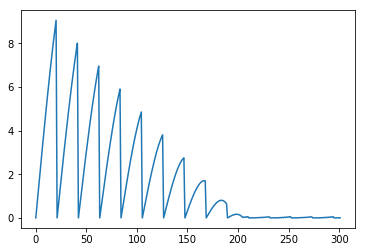
现在看看我们的拟合结果：

Y_ = w*X
plt.scatter(X, Y)
plt.plot(X, Y_)
plt.show()

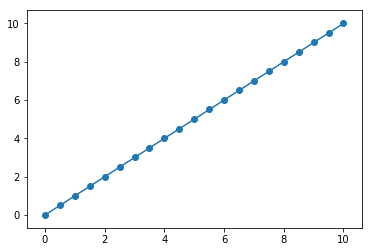
从最后的结果来看，我们的计算机成功的找(xue)到(xi)到了这个 $w$ 下一次我们试试更高维的线性回归