深度学习入门笔记(二)---多维线性回归

发表于 | 分类于
本篇将前一篇的方法进行扩展，得到了更加一般的线性回归的求解办法，而且初步展示了梯度下降的工作原理以及情况。

概览

上次我们讨论了最简单的一维线性方程的学习方法，但是大致的思路还是跟上一次很相像的，只不过这一次我们一次性要调整的参数更多、涉及的变量也比之前多一些，那么我们就准备开始吧。

公式形式

基本形式

我们的公式依旧是上篇提到的那一个：

y⃗=Wx⃗\vec y = W\vec x

其中 y⃗\vec y 是一个 nn 维的向量，x⃗\vec x 是一个 mm 维的向量，WW 就理所当然应该是一个 n×mn\times m 维系数矩阵。具体形式如下：

y⃗=[y1,y2,⋯,yn]⊤x⃗=[x1,x2,⋯,xm]⊤W=[w11w12⋯w1mw21w22⋯w2m⋮⋮⋱⋮wn1wn2⋯wnm]\begin{aligned} \vec y &= [y_1,y_2,\cdots,y_n]^\top \\ \vec x &= [x_1,x_2,\cdots,x_m]^\top \\ W &= \left[ \begin{matrix} w_{11} & w_{12} & \cdots & w_{1m} \\ w_{21} & w_{22} & \cdots & w_{2m} \\ \vdots & \vdots & \ddots & \vdots \\ w_{n1} & w_{n2} & \cdots & w_{nm} \end{matrix} \right] \end{aligned}

所以我们要调整参数就是 n×mn\times m 个。

相应的：

yi′=wi1x1+wi2x2+⋯+wimxm,i=1,2,⋯,n=∑j=1mwijxj\begin{aligned} y_i' &= w_{i1}x_1+w_{i2}x_2+\cdots+w_{im}x_m, i=1,2,\cdots,n \\\\ &=\sum_{j=1}^mw_{ij}x_j \end{aligned}

y⃗′\vec y'就是我们模型要计算的东西，现在 y⃗′\vec y' 中的每一个元素都与 x⃗\vec x 中的每一个元素有关联。

损失函数

我们依旧使用上一篇我们提到的距离，但是现在不是一个元素之间的距离，我们现在要计算 y⃗\vec y 中每一个元素与我们模型计算出来的 y⃗′\vec y' 对应元素的距离之和，即两向量之间的距离.
即：

loss=∑i=1n(yi′−yi)2loss = \sum_{i=1}^n\sqrt{(y_i'-y_i)^2}

寻求梯度

因为真实的 yiy_i 和输入 xix_i 是固定的，我们要调整的变量就是 WW 中的所有元素。
要研究每一个变量对 lossloss 的影响，我们先把 ww 暴露出来：

loss=∑i=1n(wi1x1+wi2x2+⋯+wimxm−yi)2=∑i=1n(∑j=1mwijxj−yi)2\begin{aligned} loss &=\sum_{i=1}^n \sqrt{(w_{i1}x_1+w_{i2}x_2+\cdots+w_{im}x_m-y_i)^2} \\\\ &= \sum_{i=1}^n \sqrt{(\sum_{j=1}^mw_{ij}x_j-y_i)^2} \end{aligned}

现在式子开始变得有点恐怖了，这只是为了表示方便而写的式子。我们可以尝试让 lossloss 对任取的一个 ww 求导，比如我们选择 w23w_{23}，则有：

∂∂w23loss=∂∂w23(∑j=1mw2jxj−y2)2=∂∂w23∣∑j=1mw2jxj−y2∣={x3,y2′−y2>0−x3,y2′−y2<0\begin{aligned} \frac{\partial}{\partial w_{23}}loss&=\frac{\partial}{\partial w_{23}}\sqrt{(\sum_{j=1}^mw_{2j}x_j-y_2)^2} \\\\ &=\frac{\partial}{\partial w_{23}}|\sum_{j=1}^mw_{2j}x_j-y_2| \\\\ &=\left\{\begin{aligned} x_3,y_2'-y_2>0\\\\ -x_3,y_2'-y_2<0 \end{aligned} \right. \end{aligned}

  • 第一步的推导是我们发现，在对 lossloss 求偏导时，求和符号，∑i=1n\sum_{i=1}^n 除了 i=2i=2，其他项并不包含 w23w_{23}，所以对它来说相当于常数，常数求导为 00，所以得第一个式子。
  • 第二个式子发现距离只是绝对值，我们把它取出来。
  • 第三个式子应用的原理与第一步是一样的，因为绝对值要分端求导，即可得结果。

我们就可以发现以下规律：

∂∂wijloss={xj,yi′−yi>0−xj,yi′−yi<0\frac{\partial}{\partial w_{ij}}loss= \left\{ \begin{aligned} x_j,y_i'-y_i>0\\\\ -x_j,y_i'-y_i<0 \end{aligned} \right.

我们发现求导出来的式子很简单，然后我们把所有对 ww 的偏导组合在一起成为一个矩阵，为了表示方便，我们将 ∂∂wijloss\frac{\partial}{\partial w_{ij}}loss 表示成 lijl_{ij}，则我们组合出下面这样的矩阵：

Jacobi=[l11l12⋯l1ml21l22⋯l2m⋮⋮⋱⋮ln1ln2⋯lnm] Jacobi=\left[ \begin{matrix} l_{11} & l_{12} & \cdots & l_{1m} \\ l_{21} & l_{22} & \cdots & l_{2m} \\ \vdots & \vdots & \ddots & \vdots \\ l_{n1} & l_{n2} & \cdots & l_{nm} \end{matrix} \right]

我们把上面这样对每个变量求偏导后形成的矩阵叫做雅克比( Jacobi )矩阵，上面的式子就是 lossloss 的雅克比矩阵，我们就利用它来调整 WW 矩阵。

我相信看这篇文章的人应该知道一个函数的梯度方向是其增大最快的方向，我们求出来的Jacobi矩阵就是我们梯度一种表示形式，只是之前的梯度是一行或一列的，这里是 n×mn\times m 的，如果把它展开成一列，也就成了平时看到的梯度的表示形式。

其实这种方法叫做梯度下降法，这种方法会在之后进行介绍。

学习

有了上面的认识，我们就可以用下面的式子来更新我们的 WW :

Wupdated=Wold−ϵJacobiW_{updated} = W_{old}-\epsilon Jacobi

其中 ϵ\epsilon 是上篇提到的学习率。

代码流程

整个程序还是跟之前的训练流程是一样的。

1
2
import numpy as np
import matplotlib.pyplot as plt

设定我们要学习出来的参数：

1
2
3
4
W_ = [
    [3,1,4],
    [2,3,1],
]

生成训练用的数据 X，Y

1
2
3
4
5
data_size = 1000
#这里生成了1000个三维的列向量，然后将它们拼在一起
X = np.random.uniform(0, 100,(3, data_size))
#这里生成我们训练用的准确的Y，是2x1000的矩阵
Y_ = np.matmul(W_, X)

我们用下面的函数来计算雅克比矩阵，正是应用了上面的公式

1
2
3
4
5
6
7
8
9
10
11
12
def Jacobi(X,Y,Y_):
    #y为预测值，y_为真实值
    def derivative(x, y, y_): 
        if y-y_<0:
            return -x
        elif y-y_>0:
            return x
    J = np.zeros((Y.shape[0], X.shape[0]))      #创建了一个全是0的矩阵，n行m列
    for i in range(J.shape[0]):
        for j in range(J.shape[1]):
            J[i,j] = derivative(X[j], Y[i], Y_[i])
    return J

下面就是学习的过程

1
2
3
4
5
6
7
8
9
10
11
12
13
14
W = np.zeros(W_.shape)
learning_rate = 0.0001
step_num = 5001
loss_per_step = []
for i in range(step_num):
    #获取数据
    x = X[:, i%data_size].reshape(-1,1)
    y_ = Y_[:, i%data_size].reshape(-1,1)
    y = np.matmul(W, x)
    loss = np.sum(np.sqrt((y - y_) ** 2))     #计算loss
    loss_per_step.append(loss)                #这里记录一下每一步的loss
    J=Jacobi(x, y, y_)                        #计算梯度/雅克比矩阵
    W = W - learning_rate * J                 #调整W
print(W)

看看学习出来的 WW

1
2
[[ 3.00359801  1.00038392  4.0042615 ]
 [ 2.00917684  2.99527658  1.00491496]]

与我们设定的 WW

1
2
3
4
W_ = [
    [3,1,4],
    [2,3,1],
]

已经足够接近了，如果我们把学习率调整得更低，训练的步数再适当调高，就可以得到更精确的值。

让我们看loss的变化情况

1
2
3
steps = np.array(range(len(loss_per_step)))
plt.plot(steps, loss_per_step)
plt.show()

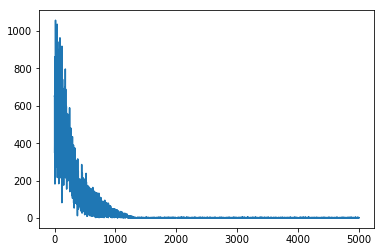
loss虽然有很多抖动，但是总体的趋势在不断减小的，最后趋向与0。

总结

这次我们看到了机器在进行学习多维线性方程的时候的表现，但是我们不禁会问，那么之前提到的形如：

y⃗=W∗x⃗+b⃗\vec y = W * \vec x + \vec b

的方程，如何才能学习到 b⃗\vec b

其实我们可以做这样的转化：
在 x⃗\vec x 的最后再添加一维，取值为 11 然后将 b⃗\vec b 拼接到 WW 的最后一列，即：

y⃗=[y1,y2,⋯,yn]⊤x⃗=[x1,x2,⋯,xm,1]⊤W=[w11w12⋯w1mb1w21w22⋯w2mb2⋮⋮⋱⋮⋮wn1wn2⋯wnmbn]\begin{aligned} \vec y &= [y_1,y_2,\cdots,y_n]^\top \\ \vec x &= [x_1,x_2,\cdots,x_m,1]^\top \\ W &= \left[ \begin{matrix} w_{11} & w_{12} & \cdots & w_{1m} & b_1\\ w_{21} & w_{22} & \cdots & w_{2m} & b_2 \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ w_{n1} & w_{n2} & \cdots & w_{nm} & b_n \end{matrix} \right] \end{aligned}

然后问题就转化到了本文讨论的问题。

虽然线性回归在机器学习以及深度学习中是比较简单的例子，但是在其中确有很大的应用，而且也可从线性回归简单的探寻到深度学习的基本工作流程。当然实际的深度学习机理要比这复杂的多，我也会在之后的学习中发表这一系列的文章。下一篇应该就是一些基本理论的介绍，不出意外应该也会一起展示的内容。