我不会详细的写出每一个概念的定义，而是采用我的理解进行叙述，如有不准确或错误的地方希望能在评论中指正
本篇涉及偏导、链式法则、概率论、信息论等的知识，因为我是参考的Deep Learning这一本书，如果有些不适的话可以去参考一下DL原书的数学部分。

概览

本篇我们来讨论一些深度学习的东西，并通过一些简单的例子来进行推导和理解。并通过代码来简单了解一下实现。

深度前馈神经网络

深度前馈神经网络顾名思义，就是当我们给定一定形式的输入的时候，数据按从输入到输出的顺序在网络中被一次性处理，中间没有数据结果在网络中反向的反馈。网络被我们分作很多层，每一层的输出都是下一层的输入，如下图：

上面是一个只有3层的深度神经网络模型，其中Layer 1，Layer 2我们称为隐藏层，Output Layer称为输出层。当然，我们的隐藏层可以更多，比如上千层。如果我们把每一层的数据操作看做是一个函数，那么我们就有如下的函数表示：

$\vec y = f^{(n)}(f^{(n-1)}(\cdots f^{(2)}(f^{(1)}(\vec x))))$

其中 $f^{(i)}$ 代表第 $i$ 层的函数。
这种思想可以想象成来源于任何复杂的函数都是由一些基本的函数构成，如指数函数、三角函数、对数函数、线性函数等等。
如高斯分布函数：

$P(x) = \frac{1}{\sigma\sqrt{2\pi}}e^{-\frac{(x-\mu)^2}{2\sigma^2}}$

如令：

$\begin{aligned} f^{(1)}(x) &= w_1x+b_1 \\\\ f^{(2)}(x) &= W_2x^2+b_2 \\\\ f^{(3)}(x) &= w_3x+b_3 \\\\ f^{(4)}(x) &= w_4e^x \\\\ f^{(3)}(x) &= w_5x+b_5 \end{aligned}$

这样， $P(x)$ 就被拆分成了一层层运算，只要调整好了参数，就可以拟合出 $P(x)$ 。

全连接

全连接的意思是神经网络的这一层的输出的每一个值都跟上一层的输出有关。如下图：

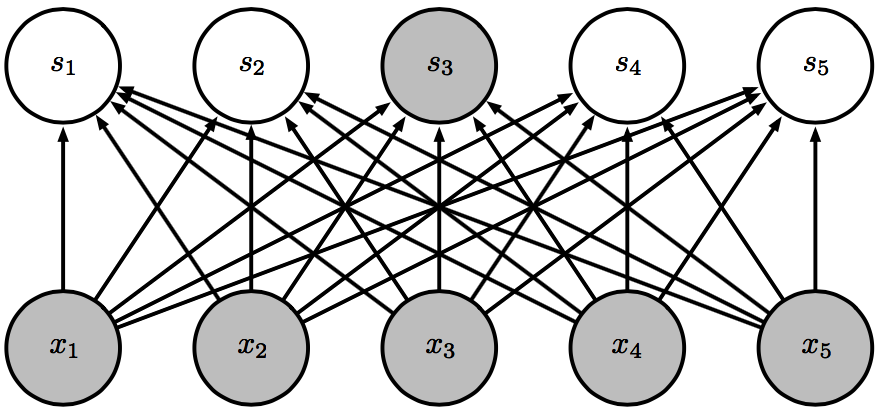
图中的每一个连线一般都是一个权重，我们一般会写成下面的式子：

$\vec s = W\vec x$

其中 $W$ 就是权重矩阵，代表着上面的连线。这个式子其实就是最简单的线性函数。

我们可以构建一个网络，然后每一层之间都用全连接的方式，这是一个非常简单的线性神经网络，但是我们可以看看这样的网络的形式是什么样的。
假设我们第 $i$ 层的权重矩阵为 $W_i$ ，置偏为 $\vec b_i$ ，输出为 $h_i$ , 网络有 $n$ 层，则：

$\begin{aligned} \vec y &= W_n(W_{n-1}\cdots (W_2(W_1\vec x+\vec b_1)+\vec b_1)+\vec b_{n-1})+b_n\\\\ &=W_{total}\vec x + \vec b_{total} \end{aligned}$

是不是很奇怪，如果全是全连接，那么我们的网络就变成了一个纯粹的线性网络，并不说这种网络没有优点，但是它所能表示的信息是比较有限的。
所以我们要对隐藏层添加一些改动。

激活函数

我们要想办法打破这种线性导致模型的表示能力(容量，只能表示线性关系)过低的情况，我们就引入一类函数，叫激活函数，它们有一些很特别的性质，让我们的神经网络更像神经网络。下面列出一些常用的函数：

线性整流单元ReLU： $h(x)=\max\{0,x\}$
Logistic Sigmoid函数： $\sigma (x) = \frac{1}{1+e^x}$
双曲正切函数： $h(x)=\tanh(x)$

他们的函数图像分别如下：

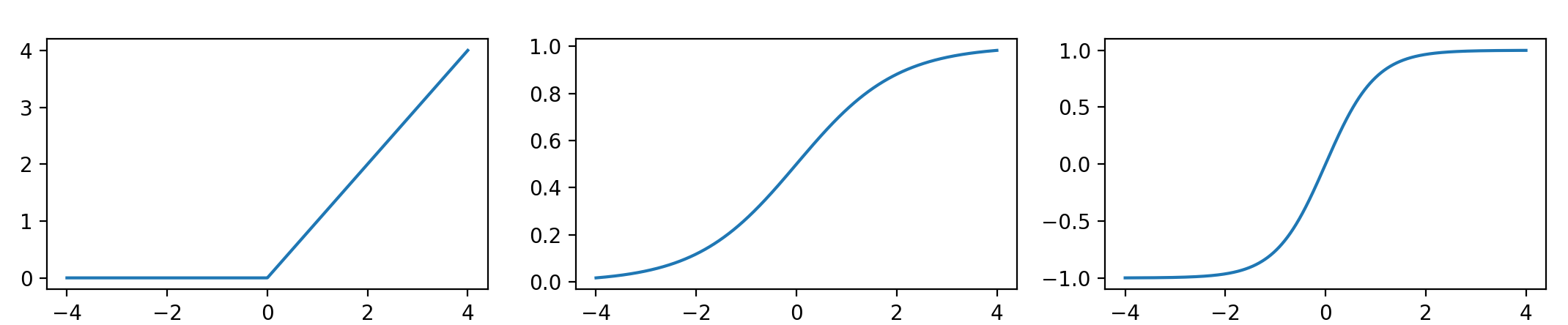
我们可以这么看待这些函数：

ReLU只有当输入大于零时才能通过
Sigmoid函数当函数大于零时有大于0.5反馈，小于零是有小于0.5的反馈，且在零的附近比较敏感，当输入很大或者很小是，它是不敏感的。它的值域是 $(0, 1)$ ，可以很好的压缩取值的范围。
双曲正切的图像可以看出跟Sigmoid函数很像，但是它的敏感区域更小，且值域是 $(-1,1)$ 。

人类的神经是通过神经间传递电流，神经对电流的敏感然后激活，再将激活传给下一个神经单元。这些函数在数值上的表现就很像人类的神经激活情况。

有了激活函数，我们就可以改善一下我们的全连接模型，在每层的链接过后，对该层的数据每个都应用一遍激活函数。这样，我们的网络就会更像一个个神经链接起来的网络，即：

$\vec h_i = \sigma (W_i\vec h_{i-1}+\vec b_i)$

其中 $h_i$ 是第 $i$ 层神经的激活状态，其他符号同之前。
现在我们的网络已经不像我们之前的线性网络了，那么它的效果怎么样的，之后会有例子说明的。

损失函数

根据之前的例子，我们使用的都是两向量的距离作为作为我们的损失函数，可以很好很直观的表现出拟合的情况。但是我们的模型的任务常常是分类和预测，我们的模型要输出的东西的意义就从数变成了概率，即我们要输出输入属于某一类或在未来的处于某种状态的概率，输入可以是一张图片、一段文本等等，输出的是图片是猫的概率或者一句话下一个单词的概率等等。我们模型的目标就成了拟合一个概率的分布函数。所以我们在函数的选择上面就要做一些调整。

概率分布

经典的概率分布

初高中我们也学了很多很经典的概率分布模型，也做过不少的题，其中就有简单的二项分布模型，如抛多次硬币，正面朝上的数量取各个值的概率；正态分布（高斯分布），概率密度函数就是上面被分解的那一个。这些我就不细数了，具体用到再说。
这里要引入一种新的分布，叫Multinoulli分布，他就像抛掷一个不均匀的色子，各面朝上的分布情况。它的各类的分布并没什么函数关系，只是纯粹表示这一类出现的概率是多少。

条件概率

条件概率表示的就是在知道一定的条件下，一个事件发生的概率。我们一般都是拟合在输入的条件下结果的分布函数。

信息熵

简单的说就是一个事件发生的概率越不可能，它的所含的信息就越高，反之，如果一个事件越有可能发生，那它所含的信息就越少，用以下的式子来定义一个事件的自信息：

$I(x) = -\ln P(x)$

我们对上面的 $I(x)$ 求期望就能的到香农熵 $H(x)$ ：

$H(x) = E(I(x)) = -\sum P(x)\ln P(x)$

KL散度

KL散度用来衡量对于相同的随机变量 $x$ 的单独的两个概率分布 $P(x)$ 和 $Q(x)$ 之间的差异，

$\begin{aligned} D_{KL}(P||Q) &= E\left[\ln \frac{P(x)}{Q(x)}\right] \\\\ &= E_{x\sim P(x)}[\ln P(x) - \ln Q(x)] \\\\ &= \sum P(x)(\ln P(x) - \ln Q(x)) \end{aligned}$

KL散度为 0 当且仅当 P 和 Q 在离散型变量的情况下是相同的分布

我们可以把KL散度看作两个概率分布之间的总距离

交叉熵

和KL散度很相似，但是缺少左边的一项：

$\begin{aligned} H(x) &= -E[\ln Q(x)] \\\\ &= - \sum P(x)\ln Q(x) \end{aligned}$

我们一般会选择交叉熵作为我们的损失函数，因为 $Q(x)$ 并不参与被省略的那一项，所以最小化它等价于最小化KL散度。一般 $Q(x)$ 是我们模型输出的概率分布， $P(x)$ 则是我们观测到的概率分布。

输出函数

对于分类的问题，一般的输出有两种，一种是用Logistics Sigmoid函数（也可以用作激活函数）来作为二类问题的输出，还有一种是 softmax 函数，可以用来输出在多个分类上的Multinoulli分布，即输出输入属于某一个类别的概率，其函数形式如下：

$softmax(\vec x)_i = \frac{e^{x_i}}{\sum^n_{j=1} e^{x_j}}$

若不对与分类，输出的函数就可以根据情况而定。

隐藏层的参数调整

调整参数的一般策略都是把损失函数看做是一层层函数参数的的函数，就像之前线性回归一样loss看作是W的函数，研究每一个参数对loss的影响，即寻找梯度，然后再调整参数。具体的求法在之后的章节中会进行说明。

总结

限于篇幅，这一篇内容就到这里，下一篇我们就用最基础东西解决一个很简单的识别任务–mnist手写数字识别。