深度学习入门笔记(四)---手写数字识别(Mnist数据集)

发表于 | 分类于
基于Mnist数据集，从一个最简单的网络来学习数据准备以及反向传播

概述

本篇将分析Mnist手写识别的从数据准备到网络构建、调整参数的各个方面来展示深度学习的一个简单应用方法。

Mnist数据集

下面是Minst数据集的简介：

The MNIST database of handwritten digits, has a training set of 60,000 examples, and a test set of 10,000 examples. It is a subset of a larger set available from NIST. The digits have been size-normalized and centered in a fixed-size image.

MNIST是NIST数据集的子集，它已经帮助我们把图片大小归一成一样的大小，并且数字一定摆在图像的中心。训练集有60000个样本，测试集有10000个样本。

数据准备

数据获取

我们可以到Mnist官网下载到数据集，数据集分成4个部分：

  • train-images-idx3-ubyte.gz: 训练集图片 (9912422 bytes)
  • train-labels-idx1-ubyte.gz: 训练集标签 (28881 bytes)
  • t10k-images-idx3-ubyte.gz: 测试集图片 (1648877 bytes)
  • t10k-labels-idx1-ubyte.gz: 测试集标签 (4542 bytes)

我们将上面的4个文件放到./MNIST_data/文件夹下，方便之后的操作。

数据提取

我们先导入我们要用的工具包：

1
2
3
import numpy as np
import matplotlib.pyplot as plt
import gzip # 用来解压gz文件

我们根据官网的对数据集的格式规定：

图像集定义
[offset] [type] [value] [description]
0000 32 bit integer 0x00000803(2051) magic number
0004 32 bit integer 60000 number of images
0008 32 bit integer 28 number of rows
0012 32 bit integer 28 number of columns
0016 unsigned byte ?? pixel
… … … …
标签集定义
[offset] [type] [value] [description]
0000 32 bit integer 0x00000801(2049) magic number (MSB first)
0004 32 bit integer 60000 number of items
0008 unsigned byte ?? label
… … … …

我们设计以下代码来提取文件中的数据：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
def read_data_set(folder='MNIST_data/'):
    # 处理32位整形数据的读取
    def _read32(bytestream):
        dt = np.dtype(np.uint32).newbyteorder('>')
        return np.frombuffer(bytestream.read(4), dtype=dt)[0]
    # 读取图片数据
    def read_image_data(filename):
        with gzip.GzipFile(folder+filename) as data_file:
            magic = _read32(data_file)
            data_size = _read32(data_file)
            rows, cols =  _read32(data_file), _read32(data_file)
            buf = data_file.read(data_size * rows * cols)
            img_data = np.frombuffer(buf, dtype=np.uint8) / 255
            # 最后除了255是为了保证像素的范围在[0, 1]之内，保证数值运算稳定
            img_data.shape = (data_size, rows, cols)
            # data_size张图片，每张图片rows行，cols列
            return img_data
    # 读取标签数据并转化成one-hot编码
    def read_label_data(filename):
        with gzip.GzipFile(folder+filename) as data_file:
            magic = _read32(data_file)
            data_size = _read32(data_file)
            labels = np.frombuffer(data_file.read(data_size), np.uint8)
            # 将标签数据转化成one-hot编码
            index_offset = np.arange(data_size) * 10
            label_data = np.zeros((data_size, 10))
            label_data.flat[index_offset+labels] = 1
            return label_data
    return read_image_data('train-images-idx3-ubyte.gz'),\
           read_label_data('train-labels-idx1-ubyte.gz'),\
           read_image_data('t10k-images-idx3-ubyte.gz'),\
           read_label_data('t10k-labels-idx1-ubyte.gz')
train_data, train_label, test_data, test_label = read_data_set()

这里涉及到一些numpy的操作，如果有疑惑的地方请自行查阅相关的文档。

上面代码的总体思路就是给定的格式将文件中的数据一个一个读取出来，图片数据就是一行28x28个整型数据，范围是0~255。最后我们调用函数将数据读出。

其中有一个比较有意思的操作是在将标签转化成one-hot向量的时候运用的技巧，算出每一个标签在数组中的其实偏移量，即index_offset，让后将目标的数据铺平后给给每个标签的位置赋值为一，即label_data.flat[index_offset+labels] = 1，这样的操作要比循环读取的速度快很多。

这段代码参考了tensorflow官方mnist教程的读取代码

为了减小每一步我们的计算量，我们将训练集用以下的生成器来将数据集分割成一定大小的分块(batch)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
def generate_batches(train_data, train_label, batch_size):
    length = train_data.shape[0]
    index = 0
    while True:
        if index+batch_size < length:
            yield train_data[index:index+batch_size], \
                  train_label[index:index+batch_size]
            index += batch_size
        else:
            tail_image, tail_label = train_data[index:], train_label[index:]
            head = (index + batch_size) % length
            head_image, head_label = train_data[:head], train_label[:head]
            yield np.ma.vstack((head_image, tail_image)), \
                  np.ma.vstack((head_label, tail_label))
            index = head

让我们把读取的数据取一部分出来看看吧：

1
2
3
4
5
6
7
8
gen = generate_batches(train_data, train_label, 1)
for i in range(9):
    image, label = next(gen)
    ax = plt.subplot(330+i+1)
    ax.imshow(image.reshape(28, 28), cmap='gray')
    ax.axis('off')
    print(label)
plt.show()

以下是输出：

1
2
3
4
5
6
7
8
9
[[ 0.  0.  0.  0.  0.  1.  0.  0.  0.  0.]]
[[ 1.  0.  0.  0.  0.  0.  0.  0.  0.  0.]]
[[ 0.  0.  0.  0.  1.  0.  0.  0.  0.  0.]]
[[ 0.  1.  0.  0.  0.  0.  0.  0.  0.  0.]]
[[ 0.  0.  0.  0.  0.  0.  0.  0.  0.  1.]]
[[ 0.  0.  1.  0.  0.  0.  0.  0.  0.  0.]]
[[ 0.  1.  0.  0.  0.  0.  0.  0.  0.  0.]]
[[ 0.  0.  0.  1.  0.  0.  0.  0.  0.  0.]]
[[ 0.  1.  0.  0.  0.  0.  0.  0.  0.  0.]]

从数据和图片不难看出one-hot编码的含义，就是数字0~9，是哪一个数字就在那一位上置1，其余都是0。从概率分布的角度来看，这就是一个Multinoulli分布，在这个位置的概率为1，依据概率分布的归一性，所以其余的位置都是0.

网络构建

我们这次的网络结构非常简单，目的有几个，一个是容易理解，二是可以在我们力所能及的范围内演示一遍运算层与层之间的运用链式链式法则求导。

网络结构

转变成数学符号，就是：

h?×10=X?×784×W784×10+b1×10y?×10=softmax(h?×10)\begin{aligned} h_{?\times 10} &= X_{?\times 784} \times W_{784\times 10} + b_{1\times 10} \\\\ y_{?\times 10} &= \text{softmax}(h_{?\times 10}) \end{aligned}

上面的公式就是我们的模型，一个全连接层加上一个 softmax\text{softmax} 输出层，其中下标表示矩阵的维数，问号表示这一维的长度不定，例如 X?×784X_{?\times 784} 表示有很多行的数据，每一行是一幅被以行优先的方式展开的图像的像素值。

因为输出的是一个概率模型，所以我们选择用交叉熵作为代价函数，调整参数，所以我们的 loss\text{loss} 的函数表达式如下：

loss=−1n∑i=0n−1∑j=09y^ijlogyij \text{loss} = -\frac{1}{n}\sum^{n-1}_{i=0}\sum^9_{j=0}\hat{y}_{ij}\log y_{ij}

其中 y^\hat{y} 是传入的标签one-hot向量。

外层的求和是求平均值，内层求和是求一行的交叉熵，nn 是一次性输入网络的图片的个数。

梯度计算

这一部分才是本篇的重点，但是你对这部分数学推导实在是没有兴趣，可以选择跳过，因为下面的内容在实际的应用中并不会出现，都是被别人包装好了的，但是为了能更好的理解，我选择在这里将过程全部展现。

我们尝试自己推导一下 loss\text{loss} 对 WW，bb 的 Jacobi\text{Jacobi} 矩阵，即梯度。

求这两个梯度要用到多维函数求导和链式法则，这里做一个简单的复习：
设有一下两个函数：

h⃗=[h1,h2]=g(x1,x2)y⃗=[y1,y2]=f(h1,h2)\begin{aligned} \vec h = [h_1, h_2] = g(x_1, x_2) \\\\ \vec y = [y_1, y_2] = f(h_1, h_2) \end{aligned}

我们要求各个 yy 对 xx 的偏导，则有如下推导式：

∂y1∂x1=∂y1∂h1∂h1∂x1+∂y1∂h2∂h2∂x1∂y1∂x2=∂y1∂h1∂h1∂x2+∂y1∂h2∂h2∂x2∂y2∂x1=∂y2∂h1∂h1∂x1+∂y2∂h2∂h2∂x1∂y2∂x2=∂y2∂h1∂h1∂x2+∂y2∂h2∂h2∂x2\begin{aligned} \frac{\partial y_1}{\partial x_1} = \frac{\partial y_1}{\partial h_1}\frac{\partial h_1}{\partial x_1}+\frac{\partial y_1}{\partial h_2}\frac{\partial h_2}{\partial x_1}\\\\ \frac{\partial y_1}{\partial x_2} = \frac{\partial y_1}{\partial h_1}\frac{\partial h_1}{\partial x_2}+\frac{\partial y_1}{\partial h_2}\frac{\partial h_2}{\partial x_2}\\\\ \frac{\partial y_2}{\partial x_1} = \frac{\partial y_2}{\partial h_1}\frac{\partial h_1}{\partial x_1}+\frac{\partial y_2}{\partial h_2}\frac{\partial h_2}{\partial x_1}\\\\ \frac{\partial y_2}{\partial x_2} = \frac{\partial y_2}{\partial h_1}\frac{\partial h_1}{\partial x_2}+\frac{\partial y_2}{\partial h_2}\frac{\partial h_2}{\partial x_2} \end{aligned}

我们把上面的式子用矩阵的方式表示，则有：

[∂y1∂x1∂y1∂x2∂y2∂x1∂y2∂x2]=[∂y1∂h1∂y1∂h2∂y2∂h1∂y2∂h2][∂h1∂x1∂h1∂x2∂h2∂x1∂h2∂x2]\left[ \begin{matrix} \frac{\partial y_1}{\partial x_1} & \frac{\partial y_1}{\partial x_2}\\\\ \frac{\partial y_2}{\partial x_1} & \frac{\partial y_2}{\partial x_2} \end{matrix} \right]= \left[ \begin{matrix} \frac{\partial y_1}{\partial h_1} & \frac{\partial y_1}{\partial h_2}\\\\ \frac{\partial y_2}{\partial h_1} & \frac{\partial y_2}{\partial h_2} \end{matrix} \right] \left[ \begin{matrix} \frac{\partial h_1}{\partial x_1} & \frac{\partial h_1}{\partial x_2}\\\\ \frac{\partial h_2}{\partial x_1} & \frac{\partial h_2}{\partial x_2} \end{matrix} \right]

即：

∇x⃗y⃗=∇h⃗y⃗×∇x⃗h⃗\nabla_{\vec x}\vec y = \nabla_{\vec h}\vec y \times \nabla_{\vec x}\vec h

如果你上面的推导不能勾起你对微积分求导时的记忆，可能你就得需要回去看看书了解一下偏导的含义了。

下面我们来看一下 loss\text{loss} 的函数组成：

h=X×W+by=softmax(h)loss=−1n∑i=0n−1y^logy\begin{aligned} h &= X \times W + b \\\\ y &= \text{softmax}(h)\\\\ \text{loss} &= -\frac{1}{n}\sum^{n-1}_{i=0}\hat{y}\log y \end{aligned}

注意上面的式子各个变量的维数。
则我们一步一步的尝试求导：

∇yloss=−1n∑i=0n−1[y1^y1,y2^y2,⋯,y10^y10]\nabla_y\text{loss} = -\frac{1}{n}\sum^{n-1}_{i=0}[\frac{\hat{y_1}}{y_1},\frac{\hat{y_2}}{y_2},\cdots,\frac{\hat{y_{10}}}{y_{10}}]

对于 ∇hy\nabla_h y， 是一个 10×1010\times 10 的矩阵，设矩阵下标为 i,ji,j 则：

when i=j:∂yi∂hi=ehi∑eh−e2hi(∑eh)2=ehi∑eh−(ehi∑eh)2=yi−yi2when i≠j:∂yi∂hj=−ehiehj(∑eh)2=−ehjehi(ehi∑eh)2=−e(hj−hi)yi2\begin{aligned} \text{when } i=j:\\\\ \frac{\partial y_i}{\partial h_i} &= \frac{e^{h_i}\sum e^h-e^{2h_i}}{(\sum e^h)^2} \\\\ &= \frac{e^{h_i}}{\sum e^h}-\left( \frac{e^{h_i}}{\sum e^h} \right)^2\\\\ &=y_i-y_i^2\\\\ \text{when } i \neq j:\\\\ \frac{\partial y_i}{\partial h_j} &= -e^{h_i}\frac{e^{h_j}}{(\sum e^h)^2}\\\\ &=-\frac{e^{h_j}}{e^{h_i}}\left( \frac{e^{h_i}}{\sum e^h} \right)^2\\\\ &=-e^{(h_j-h_i)}y_i^2 \end{aligned}

对于 ∇Wh\nabla_W h 则比较特殊，因为 WW 是一个 784×10784\times 10 的矩阵，但是对于每一个 hih_i 我们要求出对矩阵 WW 的每一个都做一次偏导，我们先将 WW 展开成一个 1×78401\times 7840 的向量，然后对其进行求导。因为 hh 是一个线性函数，所以求导就比较简单，但求出来的 ∇Wh\nabla_W h 是一个 10×784010 \times 7840 的矩阵。
从矩阵运算法则可以知道 hih_i 只与 wij,j=0,1,2,⋯,783w_{ij} , j=0,1,2,\cdots,783 有关，为了方便操作这种性质，我们把 ∇Wh\nabla_W h 的维度改成 10×784×1010\times 784\times 10，设各维的下标为 i,j,ki,j,k 则：

when i=j:∂hi∂wik=xk,k=0,1,2,⋯,783when i≠j:∂hi∂wjk=0,k=0,1,2,⋯,783i,j=0,1,2,⋯,9\begin{aligned} \text{when } i = j:\\\\ \frac{\partial h_i}{\partial w_{ik}} &= x_k, k=0,1,2,\cdots,783\\\\ \text{when } i \neq j:\\\\ \frac{\partial h_i}{\partial w_{jk}} &= 0,k=0,1,2,\cdots,783\\\\ i,j &= 0,1,2,\cdots,9 \end{aligned}

最后将其维数变回来就行。

∇bh\nabla_b h 就很简单了，一个 10×1010\times 10 的矩阵，每个元素都是 11。

最后：

∇Wloss=∇yloss×∇hy×∇Wh∇bloss=∇yloss×∇hy×∇bh\begin{aligned} \nabla_W\text{loss} &= \nabla_y \text{loss} \times \nabla_h y \times \nabla_W h \\\\ \nabla_b\text{loss} &= \nabla_y \text{loss} \times \nabla_h y \times \nabla_b h \end{aligned}

这里没有用到 ∇xh\nabla_x h 如果我们有更多的参数层的话，我们就需要用这个中间量传递到下一层来求对下一层的梯度。

梯度代码

终于把梯度求完了，让我们看看代码是怎么写的吧（其实就是对上面的公式进行应用）：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
# Y_是准确值，Y为预测值
def deff_loss_to_y(Y, Y_):
    return - Y_/Y
def deff_y_to_h(Y, H):
    deff = np.zeros((Y.shape[0], H.shape[0]))
    for i in range(Y.shape[0]):
        for j in range(H.shape[0]):
            if i == j:
                deff[i,j] = Y[i]-Y[i]**2
            else:
                deff[i,j] = -np.exp(H[j]-H[i])*(Y[i]**2)
    return deff
def deff_h_to_w(H, X):
    deff = np.zeros((H.shape[0], X.shape[0], H.shape[0]))
    for i in range(deff.shape[0]):
        for j in range(X.shape[0]):
            deff[i,j,i] = X[j]
    return deff.reshape(H.shape[0], -1)
def deff_h_to_b(H):
    deff = np.ones((H.shape[0], H.shape[0]))
    return deff
# 这个函数式对输入的X求softmax，一行求一次
def softmax(X):
    res = np.zeros((X.shape[0], X.shape[1]))
    maximum = X.max(axis=1).reshape((-1,1))
    T = X-maximum # 这里减去最大值是为了保证softmax不发生上溢
    for i in range(res.shape[0]):
        for j in range(res.shape[1]):
            res[i,j] = np.exp(T[i,j])/np.sum(np.exp(T[i]))
    return res

模型训练

训练代码

设定一些超参数以及初始化参数：

1
2
3
4
5
6
7
8
9
batch_size = 100 # 每次输入100张图片
# 用来生成batch
batch_gen = generate_batches(train_data, train_label, batch_size)
num_steps = 600 # 训练循环次数
lr = 0.1 #学习率
loss_per_batch = [] #用于记录loss的变化
# 初始化参数
W = np.zeros((784, 10))
b = np.zeros(10)

开始训练，训练的步骤依然跟以前一样，获取数据，求 loss\text{loss}，求解梯度，然后调整参数，不断循环：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
for i in range(num_steps):
    # 获取一个batch
    train_batch_image, train_batch_label = next(batch_gen)
    # 求解模型
    H = np.matmul(train_batch_image, W)+b
    Y = softmax(H)
    # 求loss
    loss = np.mean(np.sum(- train_batch_label * np.log(Y), axis = 1))
    # 上面一句的mean是对每一幅图片的交叉熵求一次平均
    loss_per_batch.append(loss) # 记录loss
    # 求梯度
    t_d_l_2_w = np.zeros((784, 10))
    t_d_l_2_b = np.zeros(10)
    # 每一幅图片都对应一个梯度，我们求其总和后求平均
    for j in range(batch_size): 
        d_l_2_y = deff_loss_to_y(Y[j], train_batch_label[j])
        d_l_2_h = np.matmul(d_l_2_y, deff_y_to_h(Y[j], H[j]))
        d_l_2_w = np.matmul(d_l_2_h, deff_h_to_w(H[j],
                            train_batch_image[j])) \
                            .reshape(-1, 10) # 这里将其变回784x10
        d_l_2_b = np.matmul(d_l_2_h, deff_h_to_b(H[j]))
        t_d_l_2_w += d_l_2_w
        t_d_l_2_b += d_l_2_b
    t_d_l_2_w /= batch_size
    t_d_l_2_b /= batch_size
    # 更新参数，注意是减去梯度
    W = W - lr * t_d_l_2_w
    b = b - lr * t_d_l_2_b
print('final:')
print(W)
print(b)

loss 的变化

用一下代码将 loss\text{loss} 的变化情况输出：

1
2
plt.plot(list(range(len(loss_per_batch))), loss_per_batch)
plt.show()

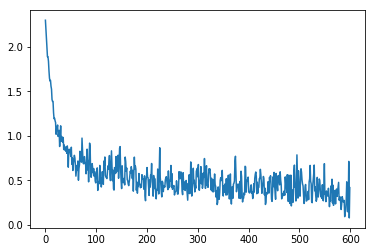
我们可以很好的看出 loss\text{loss} 的下降趋势，说明我们的训练还是很有效果的。

模型检验

最后我们要在测试集上看看我们的模型表现的怎么样，也就是计算一下模型识别的准确率如何。

我们用以下代码进行计算：

1
2
3
4
5
6
y = softmax(np.matmul(test_data, W) + b) # 这里套用我们的模型
# argmax函数给出矩阵y中最大的元素的下标，1表示每一行中的最大元素
# equal返回一个bool型的数组，表示相等或不相等
# 最后求平均就是准确率了
acc = np.mean(np.equal(np.argmax(y, 1), np.argmax(test_label, 1)))
print(acc)

上面的代码的输出如下：

1
0.9004

说明我们的模型在测试集上的有 90.04% 的准确率，识别率已经很高了。这进一步说明了我们的模型训练是有成效的。

总结

本篇的篇幅比较长，我们利用Mnist数据集进行了一次识别的演练，整个过程我们体会了深度学习从数据准备，模型的准备，调参的原理实践到观察模型变化，验证模型的整个过程，我想应该对深度学习有了更深一点的理解。
我们花了很大的篇幅在讲求导的过程，但实际上利用链式法则求导的过程在我们使用深度学习计算库的时候，他们都已经给我们做好了便捷的包装，多数我们只需要设定一下就好，而且计算效率要比我们上面的代码效率高得多。

上面的代码运行可能需要一些时间，代码都是顺序给出的，可以直接粘贴进行使用，只需安装相应的包即可，求导的计算过程可能会花费比较多的时间。如果有更高效的求法希望能指出，我个人的建议还是调用深度学习库比较稳妥，因为有比较成熟的优化。